Ardışık Sayılar Hesaplama

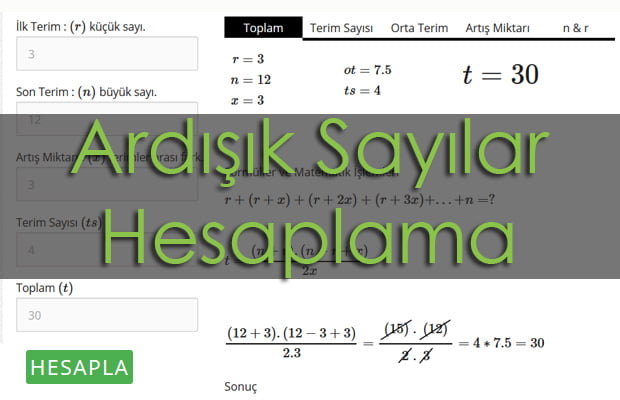
Matematiğin ana konularından olan ardışık sayılar, formüller ve hesaplamaları üzerine her türlü hesaplamayı yapabileceğiniz bir online hesap makinesi aracı. Ardışık sayılarda toplamı, orta terimi, terim sayısını, terimler arasındaki fark sayısını, ilk ve son terimi otomatik olarak hesaplayan hesap makinesi.

Formüllerde kullanılan kısaltmaların tanımları.
\(r\) : İlk terim, küçük sayı.
\(n\) : Son terim, büyük sayı.
\(x\) : Artış miktarı, terimler arası fark.
\(ts\) : Terim sayısı.
\(ot\) : Orta sayı.
\(t\) : Toplam.

Ardışık Sayılar Hesaplama Aracının Özellikleri

Giriş yapılan 3 değerden farklı olarak diğer 3 değeri hesaplar.
Ardışık sayılarda uygulanan matematik formülleri hepsi uygulanmış ve örneklendirilmiştir.
Yapılan tüm hesaplamaların formülü ile girilen değerlerin yerlerini gösterir çıktılar gösterilmektedir.
Ardışık sayılarda toplama, terim sayısı bulma, orta terim ile artış miktarı yanında en küçük sayı ilk teri ve en büyük sayı son terim hesaplaması yapılmaktadır.
Ne işe yarar.
Yapılan matematik işlemleri adım adım gösterildiğinden ardışık sayılar matematik konu anlatımı için kolay örnek oluşturulabilir.
Ardışık sayılar sorularında, çözümlerinizin doğruluğunu veya çözmekte zorlandığınız zor soruların otomatik olarak hesaplar.

Dikkat Edilmesi Gerekenler :

– En az üç değer girmelisiniz.
– Giriş yapılan sayıların tam sayı olması tavsiye edilir.
– Hesaplama formunun girişleri yukarıdan aşağıya yapılmalı, hesap hatalarını önlemek amacıyla form girişleri diğer form girişlerini silmektedir.

Sorular :

Soru 1 : Ardışık 3 çift sayının toplamı 36 ise bu dizide en küçük ve en büyük sayıların toplamı nedir?
Soruda verilen değerler; \(ts=3\), \(x=2\), \(t=36\) ise;
Sonuç : \(r\) küçük sayısı 10, \(n\) büyük sayı 14, Toplamı = 24 olacak.

Soru 2 : Ardışık iki tek sayının toplamı 28 olduğuna göre, bu sayıları bulunuz.
Soruda verilen değerler; \(ts=2\), \(x=2\), \(t=28\) ise;
Sonuç : \(r\) küçük sayısı 13, \(n\) büyük sayı 15

Soru 3 : \(2 + 4 + 6 + … + 30=?\) işleminin terim sayısını ve toplamı kaçtır?
Soruda verilen değerler; \(r=2\), \(n=30\), \(x=2\) ise;
Sonuç : \(r\) küçük sayısı 15, \(t\) toplam 240

Soru 4 : Ardışık 15 pozitif tamsayının toplamı 2085 olduğuna göre, bu sayıların en küçüğü kaçtır.
Soruda verilen değerler; \(ts=15\), \(x=1\), \(t=2085\) ise; \(r=?\)
Sonuç : \(r\) en küçük sayı 132,

Soru 5 : Aralarında 5 fark olan ardışık 25 doğal tam sayıdan en küçüğü 5 ise en büyüğü kaçtır?
Soruda verilen değerler; \(ts=25\), \(x=5\), \(r=5\), ise; \(n=?\)
Sonuç : \(n\) en büyük sayı 125,

Ardışık sayılar nasıl hesaplanır? formülleri ile yapılan hesaplama örnekleri ile online ardışıksayılar hesapmakinesi kullan. Matematik ders yardımcısı bu program ile en zor ve sayı hesaplamalarını yapabilirsiniz.